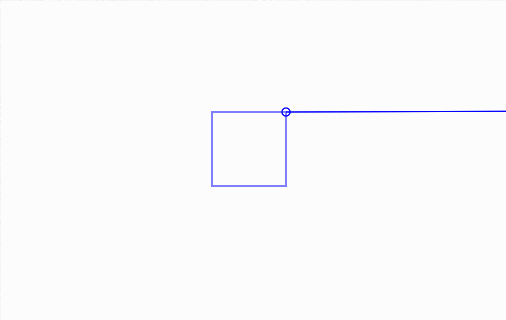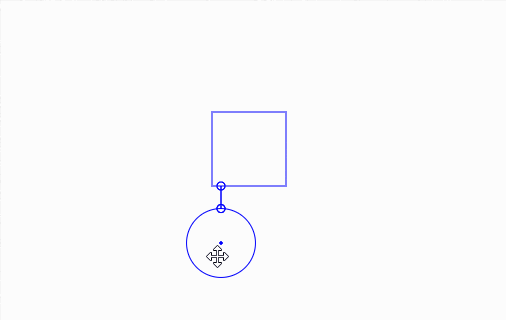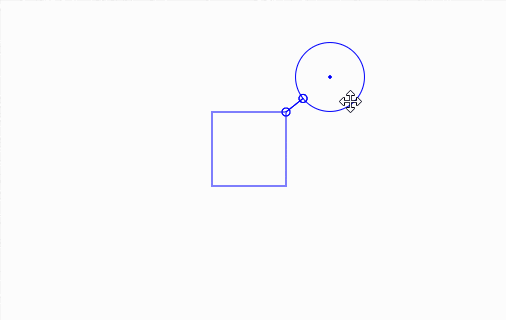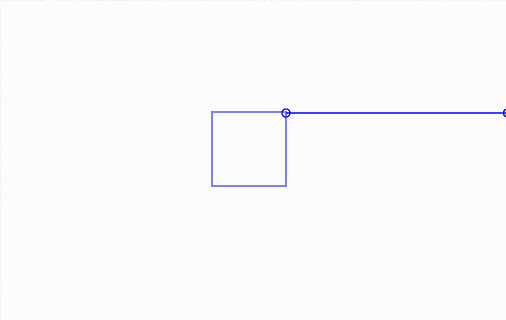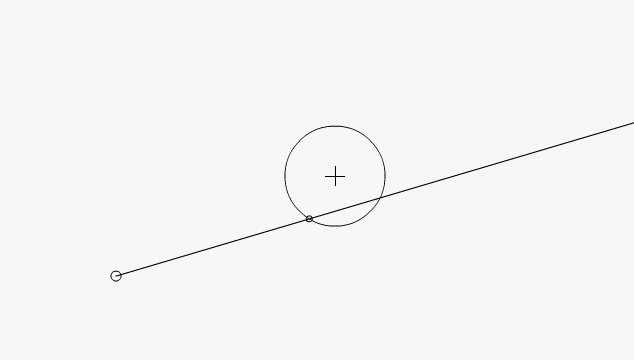
By user request on Love2d IRC channel, yesterday I've made this nice function to do intersection/collision check between a ray (for clearance, here, a ray is a infinite line with starting point but no end point) and a circle.
Underlying code is fairly simple, though it does not even require understanding to use the function.
Love2d version takes advantage of multi-return values.
Haxe version has slightly longer code due for more optimal implementation of interface.
Download Haxe .hx
Download Love2d .love
Snip:
--[[
Does a ray-circle intersection test.
Parameters:
x1, y1, di - x, y, direction (radians) of ray
x, y, r - position & radius of circle
Returns:
result - whether collision occurred
x - collision X
y - collision Y
distance - distance from ray start to collision point
]]
function ray2circle(x1, y1, di, x, y, r)
local vx = math.cos(di)
local vy = math.sin(di)
-- get relative XY of circle (relative to ray origin):
x = x - x1
y = y - y1
-- rotate it based on ray direction (as if ray starts at XY=0 and goes at +X):
local tx = x * vx + y * vy
local ty = x * vy + y * -vx
-- clear misses:
if (tx < -r) or (ty > r) or (ty < -r) then
return false, nil, nil, nil
end
-- find X coordinate that line hits rotated circle at
th = math.abs(math.cos(math.asin(ty / r))) * r
-- too far behind
if (tx + th < 0) then
return false, nil, nil, nil
end
-- line start is inside the circle:
tx = tx - th
if (tx < 0) then
return true, x1, y1, 0
end
--
return true, x1 + tx * vx, y1 + tx * vy, tx
end
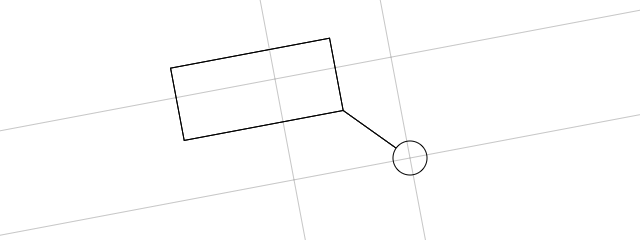 (mouseover/click to play GIF)
(click and drag to adjust rectangle size/position/rotation; distance to a circle is shown)
(mouseover/click to play GIF)
(click and drag to adjust rectangle size/position/rotation; distance to a circle is shown)