(click to interact)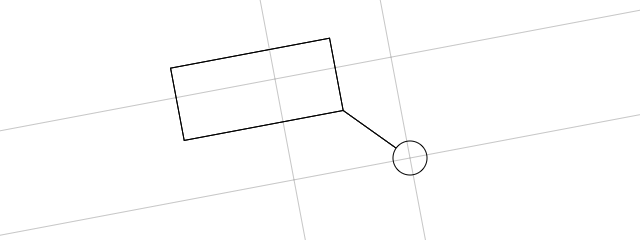 (mouseover/click to play GIF) (click and drag to adjust rectangle size/position/rotation; distance to a circle is shown)

Suppose you have a rotated rectangle and a basic shape that rotation doesn't matter for (such as a point, circle, or a line segment), and you want to check whether the two are intersecting - be that for collision handling, hit testing, or whatever else.

On a glance this might seem like a bother because things are rarely too simple with rotated rectangles, but in this case it isn't - because you can "unrotate" the rectangle.

This small post is about that.

The idea

Let's suppose you have a rotated rectangle defined by a few properties,

• Size (width and height)
• Offset to rotation center
  (that is, if this is set to 0,h/2, the rectangle would spin around the center of it's left edge)
• Position (at which the rotation center would be at any point of time)
• Rotation angle

And you have your basic shape defined by one or two (if it's a line segment) positions and perhaps a radius (if it's a circle).

If you are to subtract rectangle's position from each of the shape positions and rotate them for the opposite of rectangle's rotation angle, you would have the local coordinates for a system where the rectangle sits unrotated at 0,0 and the shape floats relative to it. At this point you can use the generally trivial intersection checks for axis-aligned rectangles/bounding boxes.

The code

The above description translates into code in a fairly straightforward way,

rel_x = shape_x - rect_x;
rel_y = shape_y - rect_y;
angle = -rect_angle;
local_x = cos(angle) * rel_x + cos(angle - pi / 2) * rel_y;
local_y = sin(angle)  * rel_x + sin(angle - pi / 2) * rel_y;

of course, as per earlier post, you can also cut the second sine/cosine call if you want,

rel_x = shape_x - rect_x;
rel_y = shape_y - rect_y;
angle = -rect_angle;
angle_cos = cos(angle);
angle_sin = sin(angle);
local_x = angle_cos * rel_x - angle_sin * rel_y;
local_y = angle_sin * rel_x + angle_cos * rel_y;

once you have local_x and local_y, you could check for intersection with a point like:

return local_x >= -rect_offset_x && local_x <= -rect_offset_x + rect_width &&
       local_y >= -rect_offset_y && local_y <= -rect_offset_y + rect_height;

or for intersection with circle (related post):

delta_x = max(-rect_offset_x, min(local_x, rect_width - rect_offset_x));
delta_y = max(-rect_offset_y, min(local_y, rect_height - rect_offset_y));
return delta_x * delta_x + delta_y * delta_y < circle_radius * circle_radius;

or any other algorithm involving an axis-aligned rectangle that spans from (-rect_offset_x, -rect_offset_y) to (rect_width-rect_offset_x, rect_height-rect_offset_y).

So a complete function might look as following (in JS and common camel-case),

function pointInRotatedRectangle(pointX, pointY,
    rectX, rectY, rectOffsetX, rectOffsetY, rectWidth, rectHeight, rectAngle
) {
    var relX = pointX - rectX;
    var relY = pointY - rectY;
    var angle = -rectAngle;
    var angleCos = Math.cos(angle);
    var angleSin = Math.sin(angle);
    var localX = angleCos * relX - angleSin * relY;
    var localY = angleSin * relX + angleCos * relY;
    return localX >= -rectOffsetX && localX <= rectWidth - rectOffsetX &&
           localY >= -rectOffsetY && localY <= rectHeight - rectOffsetY;
}

And that's about it.

Related posts:

• Love2d: Shooting things
• Variable references in GameMaker (2023 edition)
• GameMaker: Smooth pixel-perfect camera
• GameMaker: 2.3 syntax in details
• Grid-based contour traversal