(click to interact)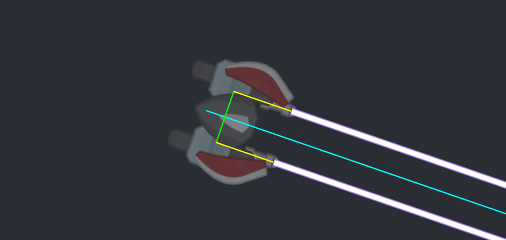
(mouseover/click to play GIF)
(spaceship graphic by Kenney)
Nowadays, most development tools provide ways of setting pivot/center point for imagery - that is, the relative point around which the image will rotate and usually be positioned relative to.
However, ability to define multiple pivot points per image remains relatively uncommon, despite being something that you want to have projectiles fire from a correct point of a sprite, display weapons/attachements at right relative points, or do anything else that demands relative offsets.
This small post is about that.
If you are familiar with basic trigonometry, you may already know that to calculate a point offset from other point in a direction, sine/cosine functions can be used, like so:
new_x = x + cos(angle) * offset new_y = y + sin(angle) * offset
(where angle is in same units as what sine/cosine functions take)
Or, if you are using GameMaker and prefer degrees instead of radians,
new_x = x + lengthdir_x(offset, angle) new_y = y + lengthdir_y(offset, angle)
and that is half of the logic here:
(click to interact)
(yellow: X offset; grab to rotate if JS is enabled)
Often enough there's an offset on both X and Y axes. The offset for the second axis would be found similarly, except adding/subtracting equivalent of 90 degrees to account for it being perpendicular to the first axis,
new_x = x + cos(angle + pi / 2) * offset_y new_y = y + sin(angle + pi / 2) * offset_y
(whether it's +pi/2 or -pi/2 depends on how your coordinate system is set up)
or with lengthdir and degrees in GM:
new_x = x + lengthdir_x(offset_y, angle - 90) new_y = y + lengthdir_y(offset_y, angle - 90)
at this point you've done most of the work:
(click to interact)
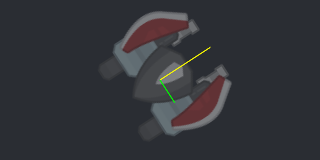(green: Y offset)
Combining the offsets on two axes is very much a matter of adding them together:
new_x = x + cos(angle) * offset_x + cos(angle + pi / 2) * offset_y new_y = y + sin(angle) * offset_x + sin(angle + pi / 2) * offset_y
or with GM
new_x = x + lengthdir_x(offset_x, angle) + lengthdir_x(offset_y, angle - 90) new_y = y + lengthdir_y(offset_x, angle) + lengthdir_y(offset_y, angle - 90)
and that's it:
(click to interact)
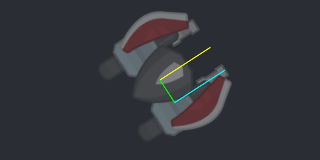(aqua: combined offset)
As an additional note here, some may find it tempting to skip over the second sine/cosine pair by using a pre-computed angle and length for offset's hypothenuse,
(click to interact)
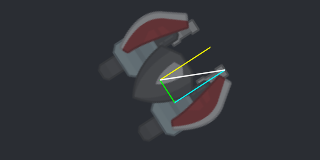(white: offset's hypothenuse)
but it isn't usually worth the bother - may instead make use of relationship between sine/cosine,
_cos = cos(angle) _sin = sin(angle) new_x = x + _cos * offset_x - _sin * offset_y new_y = y + _sin * offset_x + _cos * offset_y
and if you need to apply local scale, you can do so by multiplying the according offset,
new_x = x + cos(angle) * offset_x * scale_x + cos(angle + pi / 2) * offset_y * scale_y new_y = y + sin(angle) * offset_x * scale_x + sin(angle + pi / 2) * offset_y * scale_y
or in GM,
new_x = x + lengthdir_x(offset_x * scale_x, angle) + lengthdir_x(offset_y * scale_y, angle - 90) new_y = y + lengthdir_y(offset_x * scale_x, angle) + lengthdir_y(offset_y * scale_y, angle - 90)
to the expected effect:
(click to interact)
(white: combined offsets)
And that concludes this post!