This is a blog post about handling circle-rectangle collisions. For some reason, these seem to be generally regarded as something complicated, even though they aren't.
First things first, you may already know how to check circle-point collision - it's simply checking that the distance between the circle' center and the point is smaller than the circle' radius:
DeltaX = CircleX - PointX; DeltaY = CircleY - PointY; return (DeltaX * DeltaX + DeltaY * DeltaY) < (CircleRadius * CircleRadius);
Surprisingly or not, rectangle-circle collisions are not all too different - first you find the point of rectangle that is the closest to the circle' center, and check that point is in the circle.
And, if the rectangle is not rotated, finding a point closest to the circle' center is simply a matter of clamping the circle' center coordinates to rectangle coordinates:
NearestX = Max(RectX, Min(CircleX, RectX + RectWidth)); NearestY = Max(RectY, Min(CircleY, RectY + RectHeight));
So, combining the above two snippets yields you a 3-line function for circle-rectangle check:
DeltaX = CircleX - Max(RectX, Min(CircleX, RectX + RectWidth)); DeltaY = CircleY - Max(RectY, Min(CircleY, RectY + RectHeight)); return (DeltaX * DeltaX + DeltaY * DeltaY) < (CircleRadius * CircleRadius);
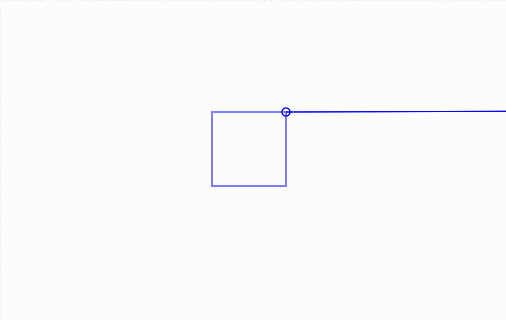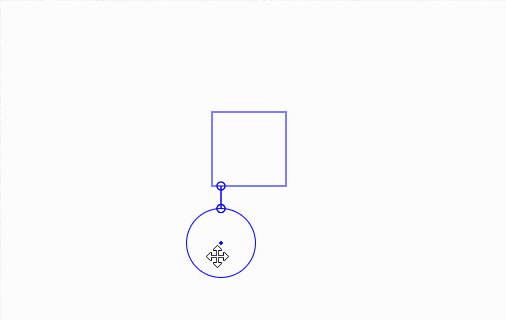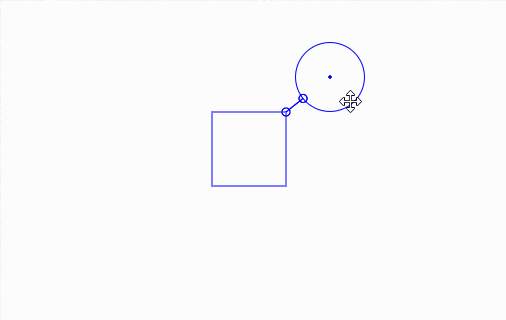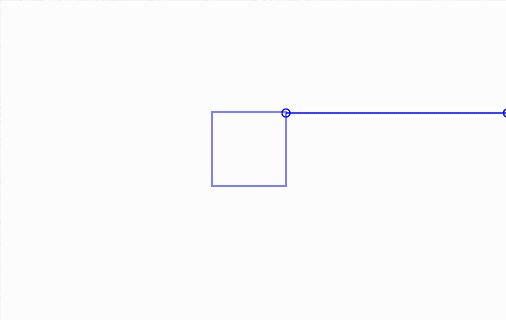
And here's it in action, along with a bit of debug drawing:
Click and drag elements.
And that is it. I've told you that it really isn't complicated, didn't I?
Bonus: Visualization ported to GameMaker
I know this is an old article but I want everyone to know that this whole thing is a lie and does not work at all how the author describes or even at all
Yep, you got me. Math as a whole is a lie – a sleigh of hand made up by mathematicians to control you.
Perhaps you’ve mixed up the meaning of rectangle coordinates as discussed in comments below?
your “find the closest point” bs does not work at all on diagonal lines
Perhaps you’d be interested in a post titled “Simple intersection checking between rotated rectangles and circles/points”
Lovely article, thanks so much!
Your posts are incredibly fantastic and instructive, and I say this both as a programmer and as a teacher / tutor… Thank you so much for your work!!
Specifically, with collisions between circles and (axis-aligned) rectangles, I was doing this weird thing where I checked all these points on the circle and on the rectangle… Very messy, ha ha! This method is so much nicer, and so clever!
What is rectX in this context? Is it the centre of the rectangle, or is it the bottom left corner?
It’s corner, not center.
WOW! This simplicity kills me! You are a frickin genius.
What do I have to change if the x and y coordinate of the rectangle is in the center of it?
Your thoughts on this?
> Fastest way is to :
– A) test circle against rect’s outer bounding circle -> reject if too far.
– B) test circle against rect’s inner bounding circle -> accept if near enough.
– C) test that the outer point of the circle (on the line joining both centers) is in the AABB.
Testing for outer point of the circle will likely cost you more cycles than this entire approach, unless you can find a way to find that point without vector normalization/trigonometry.
Your algorithm may be incomplete. what if the circle is completely inside the rectangle? circle does not intersect with the sides but it intersetcs inner of the rectangle
That is of no concern, as if the circle is inside the rectangle, the nearest point of the rectangle is in the middle of the circle. This algorithm does not make use of edge intersection checks at all.
great job! what about rotated rectangle, is it possible to extend example?
Pixon, you can translate rotated coordinates to unrotated version:
unrotatedCircleX = cos(rotation) * ( circle.x – rectCenterX ) – sin( rotation ) * ( circle.y – rectCenterY ) + rectCenterX;
unrotatedCircleY = sin( rotation ) * ( circle.x – rectCenterX ) + cos( rotation ) * ( circle.y – rectCenterY ) + rectCenterY;
Thank you very much for sharing so valuable post.
I translated your post in Chinese.
http://www.caxdev.com/2017/08/05/Math/001-Math-RectangleCircle-IntersectionTest/
May i hava your authorization? if not, i will delete the post. Thank you!
Hey, that is cool, cheers!
Where the point (RectX, RectY) is located? Bottom-Left or Top-Left?
Top-left, assuming that +x is to the right and +y is downwards.
If your coordinate system assumes +y to be upwards, it would be bottom-left instead.
Hey, so for this what does Max mean, which one of the two values is bigger, or something else?
I moved the code into java and it doesn’t work properly…
Indeed – the bigger of two arguments, not too unlike an extra line with an if-branch.
I think the only things to watch for are:
– that both objects are in same coordinate space
– that you are passing (x, y, width, height) for rectangle rather than (x1, y1, x2, y2)
– that circle radius is not negative
Big fan of your stuff, especially this article. Thank you for making it. : )
Awesome!
Thank you very much, author!
This is way to simple ^^ its something i have been thinking about for some time, but this is really qute nice :)
Hi there! I’ve been searching for ages for this! I’m not really a math person so even if this looked really simple, I can’t seem to understand how to apply this into my code. Are you willing to share the project file with me? I need to also see the debug drawing to understand it.
You can right-click on the page, pick “View source”, and scroll down to document.getElementById("canvas-605"). That’s exactly how the demo code was written – right in the blog post.
Thanks for getting back! And I just saw it. This may seem silly.. but how do I translate that into GML?
In GameMaker you wouldn’t need it at all, since there is a built-in rectangle_in_circle for this.
Here’s the demo ported to GML.
what are the rectangles points? is it the center?
It’s top-left and bottom-right corners of the rectangle – in other words, bounds of it.
Excellent algorithm, explanation and demo! Thank you for sharing it!
This is beautifully simple. Thanks for sharing it, and I love the interactive demo!