I do not know the exact name of this visual effect (angular/clockwise fade-in/fade-out?), but it is one of the most common things that you can see in interface of RPG and RTS games, displaying progress of construction/upgrade/ability cooldown. So, to the point...
You can read how this is actually being implemented, or just scroll down to the bottom of post and grab the code and/or GMK file.
Implementation of such is actually pretty simple,
1. Angle
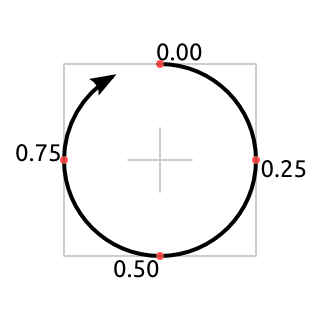
First, but still important thing to do, is to decide on a way that your code will calculate angle depending on progress. In this example, angle is being changed in a clock-like faschion (clockwise, starting and ending at top point), thus making formulae angle = PI * 2 * progress - PI / 2, where progress is a [0 ... 1] value, and angle is, well, output angle in radians, going clockwise from right-most point of a circle.
On image, cross in center indicates the zero (0, 0) point, while gray square is ((-1, -1) ... (+1, +1)) area, which final image must reside in.
Nothing complicated.
2. Make a vector
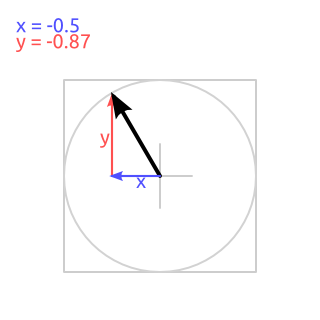
Second thing to do is to make a one-unit-long vector out of previously obtained angle. Here, "a vector" means a pair of values defining an offset. For this you will need sine/cosine functions or equivalent (even a lookup table would work, technically). In most cases this will remain as simple as x = cos(angle); y = sin(angle);. Image illustrates the resulting vector.
3. Normalize the vector
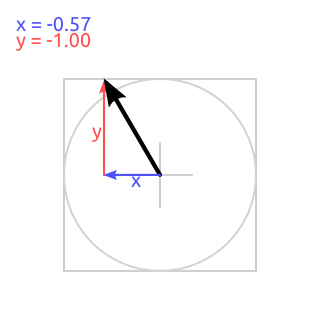
As you may or may not know, vector normalization is basically about modifying a vector to match given length while preserving direction. In this case, this is needed to make vector touch square boundary regardless of it's direction. "Touching" in this case means that either X or Y of vector must be -1 or +1. Figuring out, which of two is to be scaled, is also trivial - it's maximum of absolute values of two (l = max(abs(x), abs(y))). Afterwards, that is to be set to -1 or +1 accordingly, depending on it's original sign. The simplest (and valid) way of doing this is just to divide both of vector components by earlier found l (x = x / l; y = y / l;). After this operation, vector would look as illustrated on image.
4. Draw
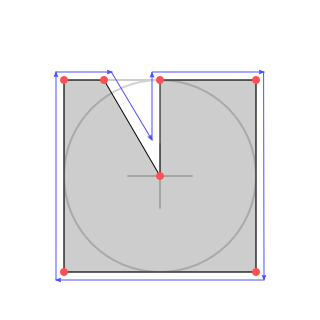
Given the normalized vector, the final task remains - it has to be drawn as actual filled shape. Fortunately, GameMaker supports a "triangle fan" primitive type, which allows to define points in fan-like order (first point is center, every next two form a triangle), making it simpler. Other programming languages and frameworks tend to support a generic "path" shape, which would be used in just about the same way. The only minimal challenge here is to draw corners of rectangle. That is normally done by adding conditional checks against pre-calculated constants. In this case, corners happen at 1/8, 3/8, 5/8 and 7/8 of overall "progress", thus leading to values 0.125, 0.375, 0.625, 0.875. As illustrated on image, shape starts at center point, goes through the points that are "behind" the current progress, goes through previously calculated vector point, and ends back at the center.
That's all the logic behind this. If something is to be cleared up, comments are welcome, since I am considerably sleepy as of typing this.
You can download example here, or use the code below. Note that example has an advantage in form of second version of script, which is compatible with GameMaker: Lite.
/// draw_rectangle_cd(x1, y1, x2, y2, value) var v, x1, y1, x2, y2, xm, ym, vd, vx, vy, vl; v = argument4 if (v <= 0) return 0 // nothing to be drawn x1 = argument0; y1 = argument1; // top-left corner x2 = argument2; y2 = argument3; // bottom-right corner if (v >= 1) return draw_rectangle(x1, y1, x2, y2, false) // entirely filled xm = (x1 + x2) / 2; ym = (y1 + y2) / 2; // middle point draw_primitive_begin(pr_trianglefan) draw_vertex(xm, ym); draw_vertex(xm, y1) // draw corners: if (v >= 0.125) draw_vertex(x2, y1) if (v >= 0.375) draw_vertex(x2, y2) if (v >= 0.625) draw_vertex(x1, y2) if (v >= 0.875) draw_vertex(x1, y1) // calculate angle & vector from value: vd = pi * (v * 2 - 0.5) vx = cos(vd) vy = sin(vd) // normalize the vector, so it hits -1+1 at either side: vl = max(abs(vx), abs(vy)) if (vl < 1) { vx /= vl vy /= vl } draw_vertex(xm + vx * (x2 - x1) / 2, ym + vy * (y2 - y1) / 2) draw_primitive_end()
Hey! Im new to developing.
How do i change the position of this effect?
The script takes arguments for where to draw it. The example draws it near the objects, but you can do whatever you’d like
I’d like to use this effect in my game, but the attached project archive file format is obsolete in modern versions of GMS2. Is there a chance vis-cooldown-rectangle.gmk could be converted to .yyz? The same is true for vis-circular-healthbar.gmk. Thanks!
The example was just the script from the post and an object calling it to showcase how it works. See the recent post on importing old files to GMS2+
will it work for gms2 also?
It will – the drawing functions didn’t change since then
For anyone who would like to achieve classic cooldown which starts filled (invert of the original example, lets say):
/// draw_rectangle_cd(x1, y1, x2, y2, value) draw_set_colour(c_red); draw_set_alpha(0.3); var v, x1, y1, x2, y2, xm, ym, vd, vx, vy, vl; v = (argument4 / 360); v = 1 - v; if (v = 0.125) draw_vertex(x1, y1) if (v >= 0.375) draw_vertex(x1, y2) if (v >= 0.625) draw_vertex(x2, y2) if (v >= 0.875) draw_vertex(x2, y1) vd = pi * (v * 2 - 1) vx = sin(vd) vy = cos(vd) vl = max(abs(vx), abs(vy)) if (vl < 1) { vx /= vl vy /= vl } draw_vertex(xm + vx * (x2 - x1) / 2, ym + vy * (y2 - y1) / 2) draw_primitive_end() draw_set_colour(c_black);Hi Lof, thank you so much for this one! I’m going to test it as soon as I’ll leave work!
You are welcome. I just wondered, how fast in fact this is? Using this metod, we draw desired semi-circular shape using only up to 5 vertexes. Normally I would render this via drawing 360 / quality vertexes (trianglefan), where quality gonna be like 64+. So the question is about speed of draw_vertex_texure function. Anyone knows the answer?
Stupid question incoming (I suck at maths, sorry :( ) : how would you do to keep the drawing a round shape instead of a square ?
The easy (and efficient) way would be to just give the primitive a texture with a circle on it. I’m meaning to make a separate post about that sometime soon.
It would be awesome!
Thanks for your answer, and waiting for your post!
Your blog is a gold mine, many thanks for that.
Hey Gary, if you are still interested in this, here is code for solution Yal mentioned. You need to create background0, would be best to be 256×256 or 200×200 at least. Place this into draw event and in create set progress = 0.
var v, x1, y1, x2, y2, xm, ym, vd, vx, vy, vl; v = progress; progress += 0.001; var tex = background_get_texture(background0); x1 = mouse_x - 100; y1 = mouse_y - 100; // top-left corner x2 = mouse_x + 100; y2 = mouse_y + 100; // bottom-right corner xm = (x1 + x2) / 2; ym = (y1 + y2) / 2; // middle point draw_primitive_begin_texture(pr_trianglefan, tex) draw_vertex_texture(xm, ym, 0.5, 0.5); draw_vertex_texture(xm, y1, 0.5, 0) // draw corners: if (v >= 0.125) draw_vertex_texture(x2, y1, 1, 0) if (v >= 0.375) draw_vertex_texture(x2, y2, 1, 1) if (v >= 0.625) draw_vertex_texture(x1, y2, 0, 1) if (v >= 0.875) draw_vertex_texture(x1, y1, 0, 0) // calculate angle & vector from value: vd = pi * (v * 2 - 0.5) vx = cos(vd) vy = sin(vd) // normalize the vector, so it hits -1+1 at either side: vl = max(abs(vx), abs(vy)) if (vl < 1) { vx /= vl vy /= vl } draw_vertex_texture(xm + vx * (x2 - x1) / 2, ym + vy * (y2 - y1) / 2, 0.5 + vx / 2, 0.5 + vy / 2) draw_primitive_end()This is really useful, thank you! One thing though, what about if you wanted a rounded rectangle? I think you would need to look at when v is between certain values for the corners, and adjust the vector length, but am not sure if it would work. Any hints?
It would certainly be easier to adapt the function to draw corners of a textured polygon instead.
Clipping the resulted graphic would be another good option.
You certainly can make a custom normalization function to fit that shape (and iterate over near-corner values to triangulate them), but I do not believe that to be a good idea for most cases.
How can I make this to fit an alarm timer?
By passing value as
1 - alarm[0] / (initial number of steps that you set alarm 0 to).Is this applicable in Haxe/OpenFL ? Or should you use a shader for this?
You could do a path via display.Graphics. A shader would probably work too, but I think a path is a simpler approach (and ideally should convert into the few needed triangles automatically).
Hey this is extremely neat. I noticed it is counter-clock-wise though. Is there an easy way to make this clock-wise?
Hey, sorry for the delayed response. The easiest way would be simply to swap x1 and x2 arguments when calling the script, causing it to draw a mirrored (and therefore CW) shape.
Thanks you very much :D Happy lucky :D
Thanks for sharing this code. I’ve used it on a personal prototyping project of mine and wish to thank you for allowing me to.
regards!
Really neat example thanks, save us from having to do all that maths again.
Sharing is caring!
Great idea for a tutorial and great scripts too. Nice of you to take the time to create a Lite-compatible version.