Angular rotation is rotation of one angle (normally a numeric value) towards other angle. This can be considered interpolation and has many applications ranging from gradual rotation towards angle to turrets, homing missiles, and procedural bone animations.
This post is about how these internally work and implementation.

Before we start

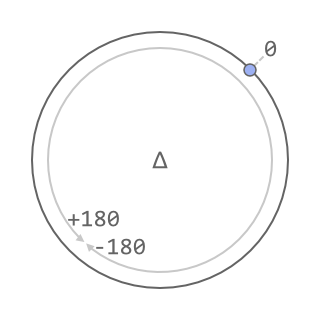
For the clarity, illustrations in this post use counter-clockwise degrees for angles, with "zero" angle facing right:

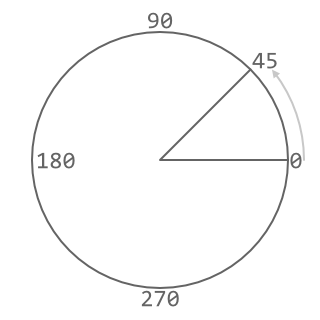
To adapt this to radians, one would have to multiply angles by -180 / pi.

The common problem

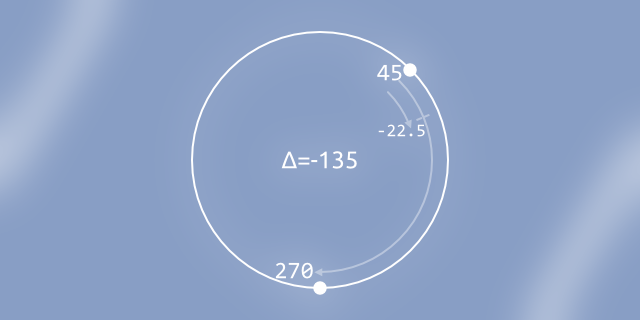
From the first look, angle rotations look easy. To rotate an angle towards other angle, we have to find difference (delta) between two, clamp it to rotation speed limits, and add with source angle.

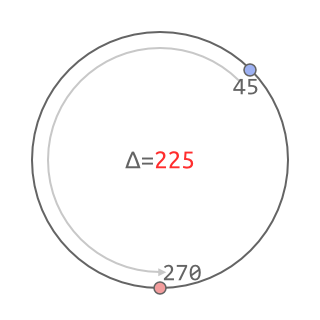
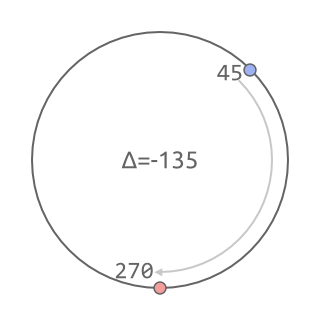
Though it's not that easy. If the input produces angles of 45 and 270, for example, above algorithm will pick the "long way", going 225 degrees instead of possible 135:

Getting it right

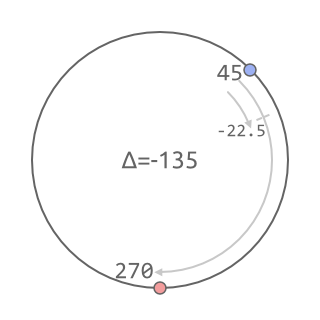
For angular rotation to work as expected, calculated delta has to be in -180 ... +180 degree range, so it doesn't take the "long way" of rotation:

This can be done by "cycling/wrapping" the value.
That is, if value goes below -180, it "comes out" from 180, and vice versa.
So if angle of 200 is passed to function, it would need to be converted to -160 to avoid rotation taking unnecessarily long way around.
Function code for cycle() would be like this in the best case:

function cycle(value, min, max) {
	var result, delta;
	delta = (max - min);
	// % is remainder-of-division operator here.
	// limit input to (-delta .. +delta):
	result = (value - min) % delta;
	// wrap negative results around the limit:
	if (result < 0) result += delta;
	// return adjusted input:
	return min + result;
}

... or this, if you prefer GameMaker:

/// cycle(value, min, max)
var result, delta;
delta = (argument2 - argument1);
result = (argument0 - argument1) mod delta;
if (result < 0) result += delta;
return result + argument1;

The idea is to limit input to (-range...+range) by using remainder of division by that, and add range to it if it's negative (so that it would stay in range).

Using it as cycle(angle2 - angle1, -180, 180) will yield us a wrapped difference of two, warranting closest rotation:

Angle rotation function itself looks like this:

function angleRotate(angle, target, speed) {
	var diff;
	// 180 is to be replaced by "pi" for radians
	diff = cycle(target - angle, -180, 180);
	// clamp rotations by speed:
	if (diff < -speed) return angle - speed;
	if (diff > speed) return angle + speed;
	// if difference within speed, rotation's done:
	return target;
}

In GameMaker, script would look like this. Not much of a difference, as you'd expect:

/// angle_rotate(angle, target, speed)
var diff;
// 180 is to be replaced by "pi" for radians
diff = cycle(argument1 - argument0, -180, 180);
// clamp rotations by speed:
if (diff < -argument2) return argument0 - argument2;
if (diff > argument2) return argument0 + argument2;
// if difference within speed, rotation's done:
return argument1;

And that's pretty much it. Once added, function is to be used like:

currentAngle = angleRotate(currentAngle, targetAngle, rotationSpeed);

And produces gradual angular rotation, as expected.

If you have a HTML5-compatible browser with JavaScript turned on, you may also observe a small demo below:

Alternatively you can take a look at jsFiddle of above demo.

Related posts:

• Variable references in GameMaker (2023 edition)
• GameMaker: Smooth pixel-perfect camera
• GameMaker: 2.3 syntax in details
• Grid-based contour traversal
• A small guide on writing interpreters, part 2